Wiskunde.net

10.
a. x = 3 of x = -3
b. x = 7 of x = -7
c. De parabool ligt boven de x-as. De lijn y = -4 ligt onder de x-as. Dus die raken elkaar nooit.
d. De parabool x² raakt de x-as in precies 1 punt (de oorsprong). Dus er is precies 1 oplossing.

11.
a. x = √13 of x = -√13 levert x ≈ 3,61 of x ≈ -3,61
b. Geen oplossingen, een kwadraat kan nooit negatief zijn.
c. x = √121 of x = -√121 levert x = 11 of x = -11
d. x = 0
e. x = √36 of x = -√36 levert x = 6 of x = -6
f. x = √1 of x = -√1 levert x = 1 of x = -1
g. x = √169 of x = -√169 levert x = 13 of x = -13
h. Geen oplossingen, een kwadraat kan nooit negatief zijn.
i. x = √0,09 of x = -√0,09 levert x = 0,3 of x = -0,3

12.
a. x = √11 of x = -√11 levert x ≈ 3,32 of x ≈ -3,32
b. x = √25 of x = -√25 levert x = 5 of x = -5
c. x = √100 of x = -√100 levert x = 10 of x = -10
d. Geen oplossingen, een kwadraat kan nooit negatief zijn.
e. Geen oplossingen, een kwadraat kan nooit negatief zijn.
f. x = √400 of x = -√400 levert x = 20 of x = -20
g. x = √4 of x = -√4 levert x = 2 of x = -2
h. x = 0
i. Geen oplossingen, een kwadraat kan nooit negatief zijn (-1/4).

13.
a. Bij t = 3,2 hoort h = 51,2 meter. Dus de hoogte van de toren is ongeveer 51 meter.
b. 5t² = 112
c. t² = 22,4 levert t ≈ 4,73 seconden

14.
a. 1/4 t² = 3
b. Links en rechts x 4 (balansmethode) levert: t² = 12, hieruit volgt: t ≈ 3,46 seconden.
c. 0,8 seconden

15.
a. x = √(20/0,1125) of x = -√(20/0,1125) levert x ≈ 13,33 of x ≈ -13,33
b. 2667 cm
c. 0,1125x² = 35 levert de lengte van de dwarsbalk: 3528 cm.

16.
a. x = 1 of x = -1
b. Geen oplossingen
c. x = 4 of x = -4
d. x = 5 of x = -5
e. x = 3 of x = -3
f. x = 9 of x = -9

17.
a. x = 0
b. x = 1 of x = -1
c. x = 5 of x = -5
d. x = 0
e. x = 5 of x = -5
f. x = 6 of x = -6
g. x = 10 of x = -10
h. x = 4 of x = -4
i. Geen oplossingen

18.
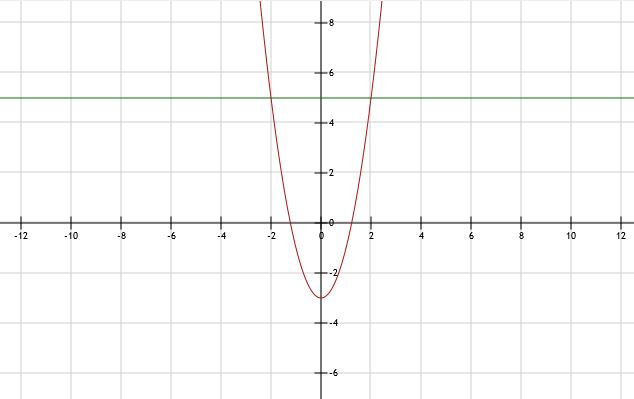
Snijpunten A(-2,5) en B(2,5)

19.
a. a = 0,000 512
b. De formule die bij de kabel hoort, is y = 0,0025x² + 15